Reliability-based design optimization for seismic structures considering randomness associated with ground motions
Abstract
When addressing the dynamic reliability analysis of structures, it becomes necessary to account for multiple limit state functions or their combinations. In scenarios where structures are subjected to random excitation, this can lead to intricate inter-dependencies among different limit states, and the computational workload can pose a substantial challenge in ensuring sufficient precision. Code-based design primarily ensures safety at the member level, while deterministic optimization fails to accommodate the inherent uncertainties associated with external excitation or the system as a whole. Therefore, in such cases, to address both the uncertainties in excitations and the presence of multiple limit states while mitigating computational challenges, equivalent extreme-value criteria are employed within the framework of the probability density evolution method to calculate the global reliability of the structure subjected to stochastic ground motions generated from the physically motivated stochastic ground motion model. Numerical optimization is subsequently conducted using genetic algorithms, aiming to minimize the cost of the superstructure while adhering to the design performance criteria related to the inter-story drift ratio and considering global reliability. Additionally, multi-objective optimization is carried out using NSGA-II, permitting the generation of multiple solutions, from which one can select the most suitable solution as needed. The numerical results illustrate the effectiveness of this technique in achieving an optimal balance between the cost of the structure and the consideration of global reliability, providing a comprehensive solution for dynamic reliability analysis and design optimization of structures under random excitations.
Keywords
INTRODUCTION
The evolution of seismic design for structures has seen continuous progress throughout history. However, a significant paradigm shift occurred in the 1980s and 90s when it was recognized that defining structural vulnerability made more sense through deformation capacity rather than strength. This realization led to a shift in seismic design from traditional force-based methods to displacement-based methods [1].
The traditional force-based approach in design codes aims to achieve two primary objectives: ensuring the safety of occupants by making structures strong and flexible and controlling structural damage by limiting excessive sway or deformation. These objectives are met through the establishment of specific design criteria. These criteria set boundaries on stress levels and forces experienced by different structural components, and they are determined based on the expected lateral forces exerted on the building during an earthquake. However, these conventional designs developed to meet these criteria often fall short of accurately quantifying their reliability. Instead, they typically rely on simple safety factors or extreme values to address this inherent uncertainty in their procedures [2,3]. On the contrary, the displacement-based design method takes a more direct approach to addressing damage compared to the force-based approach. This method emphasizes the structural performance and offers better control over the probability of surpassing critical damage states when subjected to diverse seismic excitations [4]. To support this evolving design approach, which focuses on structural performance, the Joint Committee on Structural Safety (JCSS) [5] introduced a comprehensive probabilistic model code in 1997 to determine and verify structural reliability. Similarly, the Chinese Code for Seismic Design of Buildings (GB50011-2010) [6] adopted the performance-based seismic design method and provided it as a reference for design. However, even design codes aligned with performance-based design methods often struggle to effectively account for uncertainties linked with earthquake ground motions. These approaches typically rely on a limited number of historical earthquake ground-motion records or simulated time histories that conform to the design spectrum [7,8].
Earthquakes are among the most unpredictable natural hazards, characterized by randomness in terms of return period, occurrence location, and amplitude. This inherent randomness transforms earthquake effects on engineering structures into a stochastic or random process. Neglecting this uncertainty, whether by underestimation or overestimation, can have severe consequences, ranging from structural failure to high costs. Consequently, it is imperative to rigorously quantify this uncertainty using probabilistic design principles, particularly for the analysis and assessment of stochastic systems [7,9]. In this context, reliability assessment emerges as a crucial technique, quantifying this uncertainty and determining if the structural response remains within desired limits under the influence of inherent randomness [10]. Building upon the insights derived from reliability analysis, an optimal design can then be guided through the framework of Reliability-Based Design Optimization (RBDO). RBDO aims to strike an optimal balance between reliability and cost, ensuring that structural designs are both safe and economically viable.
In recent years, a variety of reliability methods have been developed and utilized to address these challenges. Analytical approximation methods, such as the well-known First- and Second-Order Reliability Methods (FORM and SORM), involve approximating the performance function around the Most Probable Point (MPP) using linear or quadratic Taylor expansions. However, these methods may yield unreliable results when dealing with substantially nonlinear problems featuring numerous MPPs [11–13]. In contrast to the Reliability Index Approach (RIA) using the FORM, the Performance Measure Approach (PMA) became popular due to its effectiveness, particularly with the advanced mean value (AMV) technique for locating the MPP. However, challenges arise with concave performance measure functions, as AMV may face divergence issues [14–18]. Despite efforts to tackle this problem, such as the modified chaos control (MCC), MCC remains less efficient for convex performance measure functions[15,19]. On the other hand, simulation-based approaches, including Monte Carlo simulations (MCS) and their advanced versions, offer viable alternatives. MCS is recognized for its reliability and unbiasedness but suffers from slow convergence rates, particularly for low failure rates, leading to high computational costs [20]. Nonetheless, classical reliability methods, including FORM/SORM and MCS, come with significant drawbacks, such as exceptionally high computational cost and insufficient accuracy, especially when addressing dynamic responses and the seismic reliability of complex structures subjected to random excitations [8,21,22]. These challenges underscore the ongoing need for innovative and efficient reliability assessment methods. As an alternative, the Probability Density Evolution Method (PDEM), as developed by Professor Li and Chen [10,23] in the past decade, has emerged to offer improved accuracy in reliability assessment while significantly reducing computational costs. The PDEM establishes a crucial link between the evolution of the state of a system and the evolution of its probability density. This approach offers a unified framework for tackling engineering problems, whether they involve deterministic or stochastic systems. These advancements introduce a novel approach to obtaining the stochastic response and assessing the reliability of multi-degree-of-freedom systems, whether they exhibit linear or nonlinear behavior. Furthermore, they enable precise control of stochastic structural systems, both under the influence of non-stationary and non-Gaussian engineering excitations [7]. In particular, for addressing the dynamic reliability of structures with complex failure modes related to single or multiple limit states, PDEM presents an efficient approach known as the "equivalent extreme-value (EEV) event". Through PDEM, the first passage probability can be readily derived by performing a one-dimensional integral of this event [7,24,25].
Further, to investigate the reliability of structural dynamic time history analysis properly, it is essential to simulate random processes. However, in depicting real-world scenarios involving non-stationary and non-Gaussian stochastic excitations, traditional models often fall short in terms of accuracy. For instance, power spectral models, such as the Kanai-Tajimi and Kaede-Ou models, are frequently employed to simulate and generate random ground motions. Nevertheless, these models do not account for non-stationary characteristics, as they rely on stationary assumptions and fail to capture the consistent changes in ground motion over time. Additionally, they overlook the physical processes involved in ground motion generation and do not provide a comprehensive representation of the probabilistic information of original non-stationary stochastic excitations [26,27]. On the other hand, while the spectral representation method is straightforward, complete, and versatile, using the Monte Carlo method family to simulate stochastic ground motions based on the conventional spectral representation method would require an exceptionally large number of samples to achieve acceptable accuracy [28]. Therefore, to generate realistic non-stationary ground motion samples, a physically motivated stochastic ground motion model was proposed by Professor Wang and Li [26]. This model takes into account the inherent randomness associated with seismic sources, propagation paths, and local site conditions. Furthermore, the partitioning of the probability space can be done within the stochastic parameter space to select representative points for use in the PDEM. As a result, each generated representative sample is allocated a specific probability, and the collective set of these representative samples forms an all-encompassing probability dataset that serves as the source of stochastic excitation within the PDEM to facilitate in-depth structural dynamic response analysis and dynamic reliability assessment [28]. The previously discussed model is one of the approaches in current research for simulating artificial earthquakes and has been adopted in this study. However, significant advancements in the realm of synthetic earthquake generation through the application of techniques involving deep learning and artificial intelligence, particularly generative adversarial networks (GANs), are extensively explained in work by Marano et al.[29].
In addition to conducting reliability analyses, the selection of an efficient and appropriate optimization scheme is paramount in addressing RBDO problems. Within the domain of optimization, there exist gradient-based techniques, such as Sequential Quadratic Programming (SQP) and the Extended Reduced Gradient Algorithm, typically employed for solving optimization design problems. However, these algorithms heavily rely on gradient information, often resulting in localized optimal solutions. They are most suitable for optimization problems that involve continuous variables, where gradient information is readily accessible [3]. Conversely, global optimization techniques, including Particle Swarm Optimization (PSO), Differential Evolution (DE), and Genetic Algorithms (GA), offer the distinct advantage of exploring the entire design space without relying on gradient information. This approach streamlines the resolution of optimization problems that encompass discrete variables, all while facilitating the attainment of a globally optimal solution [3,30]. GA, functioning as a heuristic optimization method, explores the problem domain probabilistically and on a global scale. This approach enhances the chances of achieving solutions that are close to being globally optimal, particularly in scenarios featuring intricate problem domains [31].
In the context of addressing uncertainty and optimizing designs under uncertainty, numerous studies have emerged in recent years. Zou et al. [32] introduced an optimization technique focused on the seismic drift performance design of both fixed-base and base-isolated buildings under earthquake loads. This work was subsequently extended to encompass an automated, integrated design optimization method [33], employing the principle of virtual work to establish an explicit design problem formulation. It is important to note, however, that this particular work did not incorporate the inherent randomness associated with external excitation. An extended version of this research was presented in [34], specifically addressing the integrated RBDO of base-isolated structures, including optimization for fixed-base structures. In this study, for response spectrum analysis, earthquake action was transformed into an equivalent static action and was treated as a random variable; reliability analysis was conducted using the classical FORM, and the optimization was carried out using an Optimality Criteria (OC) method. The exploration of global reliability in structures can also be seen in the work of Lu et al. [35], where the FORM and the High-Order Moment Method (HOMM) were employed. A comparison of results between these two methods revealed that HOMM is better suited for global reliability analysis of complex engineering structures. While there are other noteworthy works in this area, each has its unique limitations. Some rely on classical reliability methods, while others lack a proper formulation of multiple limit states. Additionally, certain studies neglect the physical mechanisms of earthquakes during the simulation of random seismic events. Hence, there is a growing need for a seamless RBDO procedure capable of mitigating all these limitations. Nevertheless, there are also notable works that have their own way of accessing optimal designs, as seen in the work of Castaldo et al. [36] where equation of motion is implemented in non-dimensional form considering PGA to PGV ratios for optimal design of FPS bearings.
To illustrate the rationale behind the adoption of stochastic ground motions and the utilization of the PDEM for RBDO, several notable contributions in this field have been referenced. The foundational model of the physically motivated stochastic ground motion was initially introduced by Professors Wang and Li in their work [26]. Building upon this model, Peng et al. [8,37] have applied it in various studies, employing it for generating stochastic ground motions and conducting RBDO and probabilistic analyses for adaptive sliding base isolation systems and base-isolated structures with sliding hydro-magnetic bearings. Additionally, this ground motion model has been used alongside the absorbing boundary condition of PDEM to facilitate the probabilistic optimization of TMDI (Tuned Mass Damper-Inerter) systems, as demonstrated by Sun et al. [38]. Furthermore, the realm of stochastic optimal control for physical stochastic systems has been extensively explored through the application of PDEM, as detailed in the book authored by Peng et al. [7]. These references collectively underscore the significance and versatility of stochastic ground motion modeling and the PDEM framework in addressing complex problems related to reliability and optimization in structural engineering.
In this study, RBDO for a planar frame structure is conducted. This is achieved by combining the EEV event criteria in the PDEM with GA. The aim is to secure the structure against interstory drift ratios under non-stationary external excitations. To achieve this, the concept of global reliability, synonymous with system reliability, is employed to accommodate multiple limit states associated with interstory drift across all floors. In Section 2, the generation of physically motivated stochastic ground motion and the subsequent reliability analysis using PDEM for the generated random ground motions are detailed. Section 3 outlines the RBDO problem formulation, including the chosen design variables, objectives, and constraints. The later sections present the results of deterministic optimization and RBDO using GA, with further comparisons of the outcomes. Moreover, the NSGA-II algorithm is applied to provide the advantage of selecting the desired design from the feasible solution set, resulting in an efficient and flexible optimal design solution for structures subjected to random ground motions.
RELIABILITY ASSESSMENT OF A LINEAR STOCHASTIC DYNAMICAL SYSTEM
In the context of a linear structural system with
In this expression, M, C, and K represent n*n matrices corresponding to mass, damping, and stiffness, respectively. The acceleration, velocity, and displacement of the system are denoted as n-dimensional column vectors, represented as
Modeling of stochastic ground motion
In Equation (1), the random input term
where,
Here, the random parameter vector
The model outlined above addresses the stochastic nature of acceleration at the bedrock and the specific characteristics of the site's soil. To derive the input at the bedrock, a comprehensive integration of seismic source effects and wave propagation is conducted, guided by seismic hazard analysis. In this approach, the soil layer is effectively represented as an equivalent linear single-degree-of-freedom system, as shown in Figure 1. Subsequently, seismic excitation is applied at the base, and the absolute response of this system serves as an accurate representation of the seismic ground motion process. As a result, ground motions can be reliably simulated using a simplified theoretical formula that captures the physical relationship between surface ground motions and input motions at the bedrock while considering essential parameters such as the predominant circular frequency and equivalent damping ratio as depicted below[7,27,39]:
where
The frequency domain equation of ground motion data presented in Equation (5) can now be obtained in terms of time domain by performing inverse Fourier transfer of this equation [39].
The time history of ground acceleration obtained from Equation (6) can be further enhanced by adding non-stationary characteristics. This is done using a uniform modulation function as follows [10]:
Probability density evolution method
In this study, a structural reliability analysis employs the PDEM introduced by Li and Chen [23]. Based on the probability conservation principle, this method is proficient at capturing the probability density function (PDF) of structural responses in the presence of random excitations and associated uncertainties at any given time instant [7,8,40].
In the context of a dynamic system, the likelihood of surpassing a predefined limit state can be characterized as the first passage probability. This helps us understand the probability of the system crossing a specific point within a certain time, providing insight into the system reliability[10,41]. The dynamic structure reliability associated with the first-passage problem under stochastic ground motions is defined as:
where
The above definition of reliability holds when there is involvement of a single limit state function only, i.e., when a single mode of failure is considered or when only one member or element of the structure fails. However, when assessing the reliability of a structure, we typically need to consider multiple modes of failure or multiple failures of elements, as represented by the following equation [7,10,37]:
where
The above equation (Equation (9)) can be solved using commonly employed reliability theory based on the level-crossing process. However, this theory often struggles to ensure accuracy, and its procedure is not straightforward or convenient due to the requirement of the joint PDF of the response and its velocity for reliability assessment, along with the need to assume properties of the level-crossing events. Consequently, in this study, a more efficient method, devoid of the mentioned issues, is employed to assess dynamic reliability. This method transforms the problem into an EEV scenario, as detailed in [24,25]. By calculating the probability of such an EEV event, it becomes possible to evaluate the probability of compound random events involving combinations of more than one inequality.
The EEV event can be constructed in terms of random variables as:
Now, Equation (9) can be defined alternatively in terms of EEV as:
It can also be written in an integral form as:
where
The equation above illustrates how system reliability, which involves a high-dimensional integral, can be simplified to a one-dimensional integral through the establishment of the EEV event.
The extreme value distribution or the PDF of this EEV event can be characterized by constructing a virtual stochastic process as follows:
The virtual stochastic process is to ensure that its extreme value coincides with the value of the virtual stochastic process at a specific time point, denoted as
The variables used in the equation are defined as follows:
In this context, the constructed pseudo-random process
Here, both the pseudo-random process
The initial condition for the above partial differentiation equation is given by:
where
To derive the solution of
where
Now, to determine the PDF of the EEV event,
Numerical procedure for solving the first-passage problem using PDEM
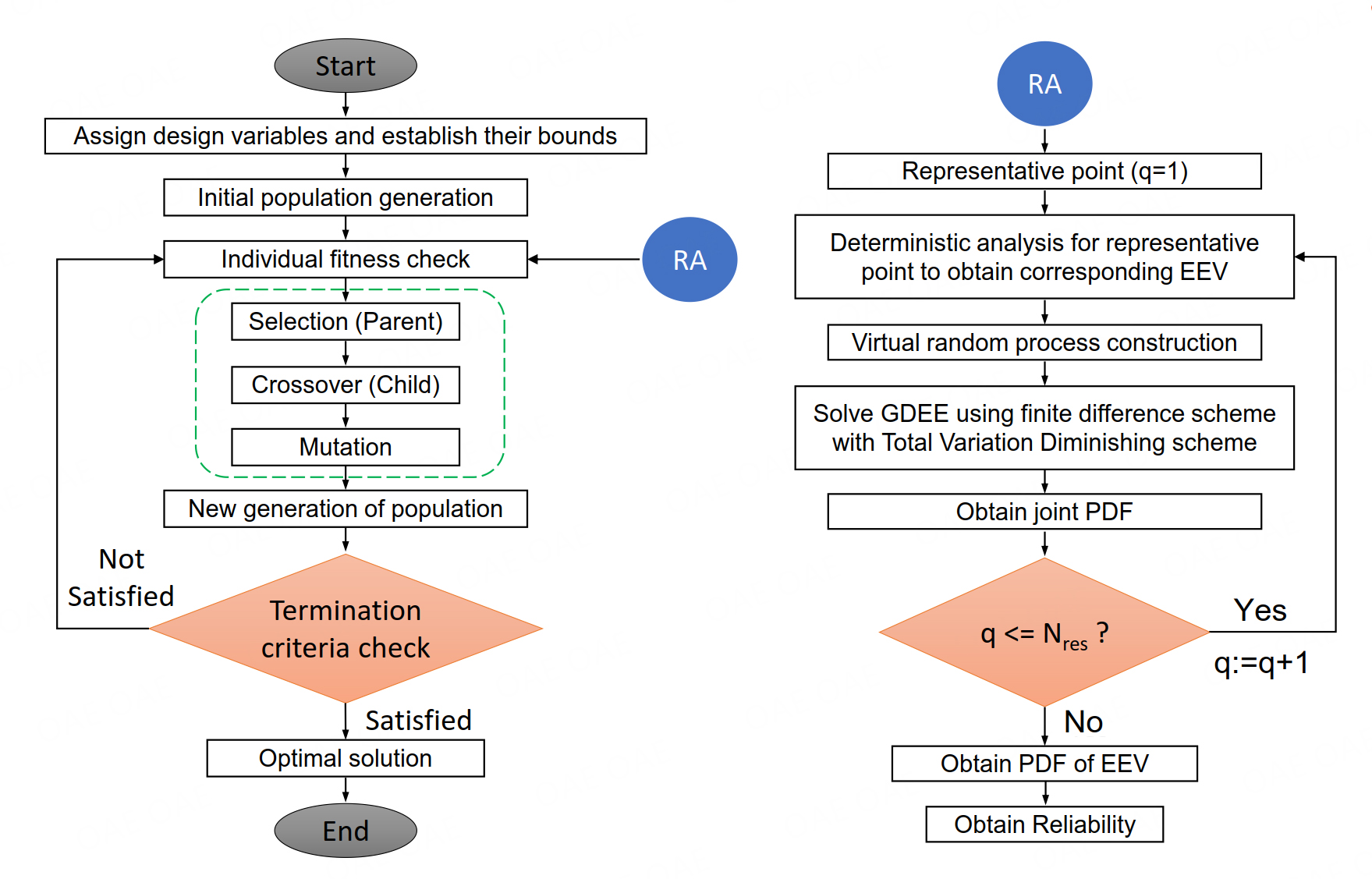
The theoretical derivation mentioned above can be explicitly expressed in terms of a combination of steps as mentioned below. The following algorithm first evaluates the first passage probability using PDEM, ultimately resulting in the structural reliability.
Step 1: Selection of representative points: Partition the probability space of the random vector
Step 2: Deterministic structural analyses: For each representative point
Step 3: Solve GDEE: Compute the velocity term of the pseudo-random process by taking its derivative and incorporating it into the GDEE presented in Equation (15). For each
Step 4: Reliability evaluation: Derive the PDF
RELIABILITY-BASED DESIGN OPTIMIZATION
When dealing with problems related to uncertainty and randomness, as opposed to deterministic design approaches, it is important to undertake a reliability assessment for the resultant design—whether it is in the form of a preliminary design or a finalized iteration. However, within the realm of structural design, neither an excessive abundance of reliability nor an insufficiency in it is sought. The former could lead to inflated costs, while the latter could pave the way for structural failure. The traditional iterative trial-and-error approach to finding an optimal solution is not only imprecise but also time-intensive. Thus, to strike a balance between cost and reliability, a more effective avenue is the adoption of RBDO. This method constitutes an automated process that seamlessly integrates both reliability assessment and optimization procedures.
To establish the RBDO framework, the following factors should be incorporated into the RBDO scheme:
Design variables
In a structural system with a fixed base, the pivotal role of distributing loads and maintaining stability falls upon components such as beams, columns, and slabs. The source of uncertainty in this study is the external excitation and the structural geometry uncertainties are not considered; therefore, given a pre-determined topology and layout of the superstructure, the dimensions of these structural members can be regarded as deterministic design variables within the framework of the superstructure's design. However, sometimes epistemic uncertainties do affect the RC structures, which should be considered in the analysis, as explained in [42]. When dealing with rectangular members, their cross-sectional property, such as the moment of inertia (
Design Objective
The fundamental aim of this study is the minimization of construction costs pertaining to the superstructure. In scenarios involving a structure composed of
While formulating the design objective, it is essential to properly consider the uncertainties associated with the objective function within the RBDO procedure. However, due to the lack of reliable cost data, it is generally acceptable to treat the cost function as deterministic, and this study also adopts this approach. The design objective is, thus, formulated as:
Here,
Design constraints
In this study, the primary design constraint for evaluating system reliability revolves around the global reliability of interstory drift ratios. Specifically, this constraint does not solely focus on the inter-story drift ratio between particular floors, such as drift ratios between the first and second floors, but instead encompasses a broader scope called "global reliability", necessitating that all other inter-story drift ratios remain below their corresponding thresholds ensuring the reliability of the specified parameter to remain above a designated threshold. This threshold might be established through a probabilistic model code or chosen based on specific performance criteria. The assessment of the reliability of this parameter is conducted through the methodology outlined in Section 2.2 and Section 2.3.
Here,
RBDO problem formulation
Once the reliability threshold is established and the reliability is computed through the process outlined in Section 2.3, the RBDO scheme is formulated as a mixed continuous-discrete optimization problem, expressed as:
In the above equation,
This study employs the GA within the pymoo module [44] in Python for optimization. The GA iteratively evaluates design solutions by creating an initial population, calculating failure probabilities, and analyzing reliability based on the constraints. Solution fitness is determined by their reliability, and reproduction is driven by selection, crossover, and mutation. Offspring also undergo reliability analysis, and this iterative process continues. The algorithm aims to find solutions that balance cost and reliability, aiming for designs to meet performance and safety requirements while fulfilling other criteria.
Reliability-based design optimization procedure
Step 1: Set initial values for the deterministic design variables and establish their corresponding bounds. Additionally, first, set the allowable limit and determine the targeted reliability for the specific parameter of interest, namely, the interstory drift ratio.
Step 2: Conduct structural analyses using the stochastic ground motions generated based on the principles detailed in Section 2.1 for the design variables. Calculate the drift ratio for each floor and record the maximum drift ratio among all floors at each time interval for further analysis.
Step 3: Perform reliability analysis using PDEM, as detailed in Section 2.3, to evaluate the global structural reliability against interstory drift ratios.
Step 4: Based on the results of reliability analysis, formulate the RBDO problem, as mentioned in Equation (22).
Step 5: Adopt the GA to perform the optimization procedure. Within each population, the algorithm adjusts the width
Step 6: End the design optimization procedure when the designated termination criterion for a solution is met. If not, proceed to Step 2 for the subsequent design iteration.
The procedure described above is depicted in a flowchart shown in Figure 2.
ILLUSTRATIVE EXAMPLE
To showcase the practical implementation of the aforementioned methodology, a structural example from the work of Zou et al. [34] has been employed. For this analysis, the structural topology, layout, material properties, and story masses across all levels are retained to be identical as in the work of Zou et al. [34]. However, to investigate system reliability under the impact of dynamic stochastic loads, the input loads have been modified.
Initially, deterministic optimization is performed for static loads, following the seismic design response spectrum outlined in the Chinese seismic design code (GB50010-2010) and is termed 'Case A'. Subsequently, a reliability analysis is conducted using the PDEM with stochastic ground motions consistent with the site class and seismic intensity used in the deterministic optimization. Recognizing the inadequate reliability of deterministically optimized structures, optimal reliability is pursued through RBDO and is termed 'Case B'. This approach integrated PDEM with GA to achieve an optimized design that ensured the desired level of reliability. Recognizing the necessity for adaptable optimization approaches, a multi-objective optimization employing NSGA-II was pursued, facilitating the creation of a Pareto solution set. This allows for a range of solutions, providing the flexibility to strike a balance between cost and reliability as needed.
The exampled structure comprises a ten-story two-bay planar frame with its base fixed on the ground, as shown in Figure 3A. Each story has an assigned mass of
Figure 3. Structural layout and design spectrum. A: Ten-story two-bay planar concrete frame; B: Design spectrum (
Comparison of Optimal Member Sizes
| Minimum requirement | Case A (DO) | Case B (RBDO) | ||||||||
| Initial sizes | Optimal sizes | Optimal sizes | ||||||||
| Element type | Storey level | Member group | Width (mm) | Depth (mm) | Width (mm) | Depth (mm) | Width (mm) | Depth (mm) | ||
| Column | C1, C3 | 300 | 300 | 300 | 300 | 300 | 301 | |||
| C2 | 300 | 300 | 300 | 844 | 300 | 1400 | ||||
| C1, C3 | 300 | 300 | 300 | 300 | 300 | 301 | ||||
| C2 | 300 | 300 | 300 | 776 | 300 | 1083 | ||||
| C1, C3 | 300 | 300 | 300 | 571 | 300 | 1255 | ||||
| C2 | 300 | 300 | 300 | 300 | 300 | 310 | ||||
| C1, C3 | 300 | 300 | 300 | 537 | 300 | 771 | ||||
| C2 | 300 | 300 | 300 | 300 | 300 | 325 | ||||
| C1, C3 | 300 | 300 | 300 | 300 | 300 | 305 | ||||
| C2 | 300 | 300 | 300 | 550 | 300 | 851 | ||||
| Beam | B1, B2 | 250 | 350 | 250 | 689 | 250 | 744 | |||
| B1, B2 | 250 | 350 | 250 | 709 | 250 | 830 | ||||
| B1, B2 | 250 | 350 | 250 | 628 | 250 | 621 | ||||
| B1, B2 | 250 | 350 | 250 | 542 | 250 | 751 | ||||
| B1, B2 | 250 | 350 | 250 | 406 | 250 | 556 | ||||
| Reliability | - | 0.41307 | 0.89534 | |||||||
| Cost (Kg) | 46782.5 | 74813.6 | 98235.4 | |||||||
Deterministic Optimization
To initiate deterministic optimization, lower-bound depths and widths were adopted from Zou's prior study [34]. For beams and columns, the depths are set at a minimum of
A response spectrum modal analysis is conducted to determine the peak modal displacements. The Square Root of the Sum of Squares (SRSS) rule, known for its accuracy in two-dimensional problems, is employed to combine the first five peak modal responses [46]. Subsequently, the inter-story drift ratio is computed as the ratio between the difference in lateral displacement of
The optimal design problem is defined in a manner consistent with the RBDO formulation presented in Equation (22). The only distinction is that the reliability constraint is replaced by a deterministic constraint, which is expressed as follows:
where
The design optimization process aims to minimize the cost function, as described in Equation (20), ensuring that the maximum inter-story drift among all floors remains below the threshold of
Results of Deterministic Optimization
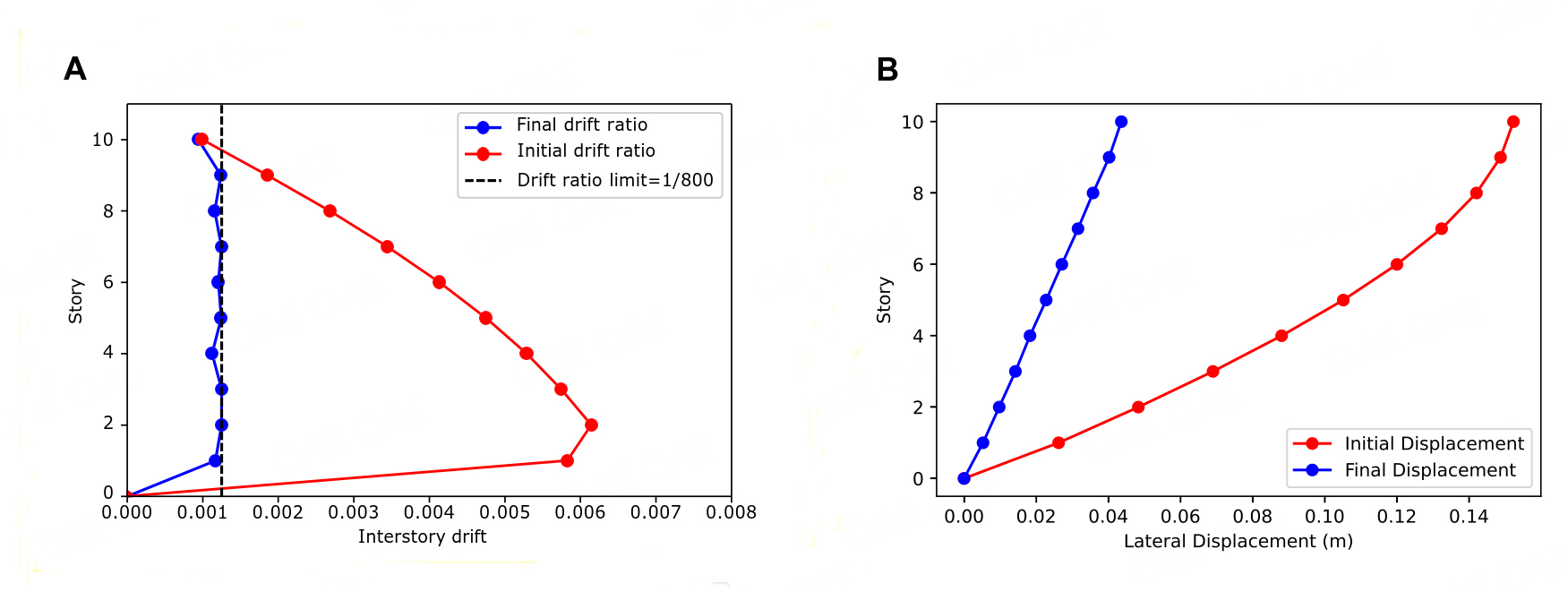
The initial structure, adopted with minimal member sizes to ensure basic constructability requirements [34], failed to meet multiple inter-story drift ratio criteria, leading to excessive flexibility, longer vibration periods, lateral displacement, and drift violations, as shown in Figure 4 and Table 2. After optimization, the member depths of the structure increased, making it stiffer, as shown in Table 1. This reduced lateral displacement across all floors and reduced the period of the first mode of vibration from 3.86 seconds to a suitable 1.5 seconds (as shown in Table 2). The increased member size also raised the structural cost (seismic weight) from the initial 46, 782.5 kg to 74, 813.60 kg for the optimal configuration. However, this cost increase is justified by the significant reduction in lateral displacement and drift ratios, which are now within acceptable limits, as shown in Figure 4.
Figure 4. Responses of deterministic optimization. A: Initial and final inter-story drift ratios; B: Initial and final lateral displacement profiles
Comparison of natural periods of vibration
| Initial sizes | Case A | Case B | |
| Mode | Period (sec) | Period (sec) | Period (sec) |
| 1 | 3.86 | 1.528 | 1.064 |
| 2 | 1.274 | 0.598 | 0.383 |
| 3 | 0.75 | 0.359 | 0.233 |
| 4 | 0.522 | 0.245 | 0.15 |
| 5 | 0.395 | 0.183 | 0.137 |
Although Figure 4A illustrates that all floor drift ratios are well within acceptable limits post-optimization, it is essential to note that this optimization process does not consider uncertainties in external excitation or the system. Therefore, the reliability of this optimal solution remains unverified. Relying solely on deterministic optimization would necessitate an exceptionally high safety factor, leading to a rapid escalation in costs without guaranteeing reliability. Therefore, to address this concern and thoroughly assess the reliability of the optimized structure, a comprehensive reliability assessment is conducted in the subsequent section.
Reliability Assessment of optimal results from deterministic optimization
The optimal structure obtained from Section 4.1 is subjected to random ground motions derived using the physically motivated stochastic ground motion model detailed in Section 2.1 to incorporate the randomness within the external excitation. Subsequently, the global reliability of the structure with respect to the inter-story drift ratio is assessed through the utilization of PDEM.
Generation of stochastic ground motion
As detailed in Section 2.1, the two principle sources of randomness are defined as randomness in site soil and randomness in acceleration at bedrock. To evaluate the former, an engineering site is considered, characterized as site class
In this study, PDEM, as described in Section 2.2, is utilized to perform reliability analyses on structures exposed to random ground motions. The initial step involves choosing representative points within the stochastic parameter space. Subsequently, the physical stochastic model outlined in Section 2.1 referred from [7] is employed to generate ground motion acceleration time histories. The tangent spheres method is then used for partitioning the probability space, resulting in the selection of 221 representative points. The generated ground motions have a sampling frequency of 50 Hz and a total duration of 20.48 s. To capture the non-stationary characteristics of these ground motions, Equation (7) is applied, with values of
Now, the seismic load utilized in both deterministic optimization and stochastic analysis corresponds to the same site conditions and seismic intensity. To confirm their consistency, statistical properties of the response spectrum of these stochastic ground motions are computed. Figure 5A depicts the mean and the mean plus one times the standard deviation plotted against the design spectrum. The mean response spectrum is scaled to match the design spectrum, and it is evident that the calculated mean plus one times the standard deviation encompasses the entire design spectrum, affirming their validity. Additionally, the model effectively captures the non-stationary characteristics of the time histories and the sample-to-sample variation, with one representative time history illustrated in Figure 5B.
Results of Reliability Assessment
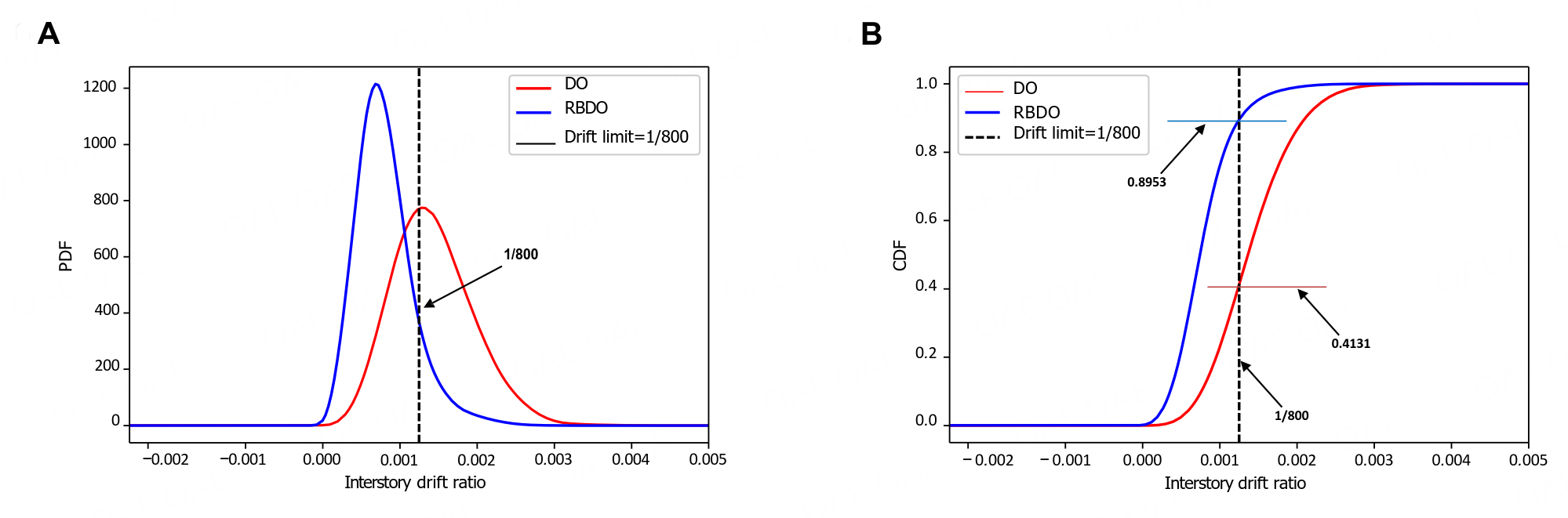
The PDF and Cumulative Density Function (CDF) of the EEV interstory drift ratio resulting from the structure's exposure to stochastic ground motions are depicted in Figure 6. In contrast to the work of Zou, where reliability indices were employed, PDEM quantifies target reliability in terms of percentages. For this study, the target reliability in PDEM is set at 0.886, which corresponds to a reliability index of 1.2 in his study. This determination is made using a first-order approximation of the failure probability, which is calculated as the probability content of the half-space in the standard normal space, as described in the following equation [16,47]:
Figure 6. PDFs and CDFs of deterministic and reliability-based optimized structures subjected to stochastic ground motions. A: probability density functions; B: cumulative density functions
where
The red curve in Figure 6B illustrates the CDF of the structure optimized deterministically. It is evident that with a drift ratio of 1/800, the reliability is only 0.41, which falls significantly below the target reliability. Examining the PDF curve depicted in Figure 6A, it becomes apparent that the probability of exceeding the drift limit is approximately 50%, a value considerably higher than the targeted exceedance probability. These results underscore the inadequacy of the deterministic optimization technique. Consequently, the subsequent section focuses on optimization while enforcing the constraint of drift ratio reliability.
Reliability-based design optimization
Single-objective optimization using GA
To initiate the RBDO procedure, the initial and final bounds, material properties, and structural configuration remain consistent with those in deterministic optimization. However, a fundamental distinction arises from the incorporation of random ground motions, resulting in a stochastic process. The central concept is to design an optimal structure in which the maximum interstory drift ratio remains within the permissible failure probability, ensuring global reliability where all limit states fall within safe margins. To achieve this, the concept of global reliability is integrated using the EEV event approach. In this context, the limit state of each floor must be considered. Consequently, the maximum drift ratio among all floors is evaluated for each representative point, as formulated in Equation (9). PDEM is then readily applied to obtain the PDF and CDF of the inter-story drift ratio. RBDO is a two-step optimization procedure; the inner loop is dedicated to reliability analysis, and the outer loop is focused on structural optimization. This process is mathematically defined in Equation (22), with a primary constraint stating
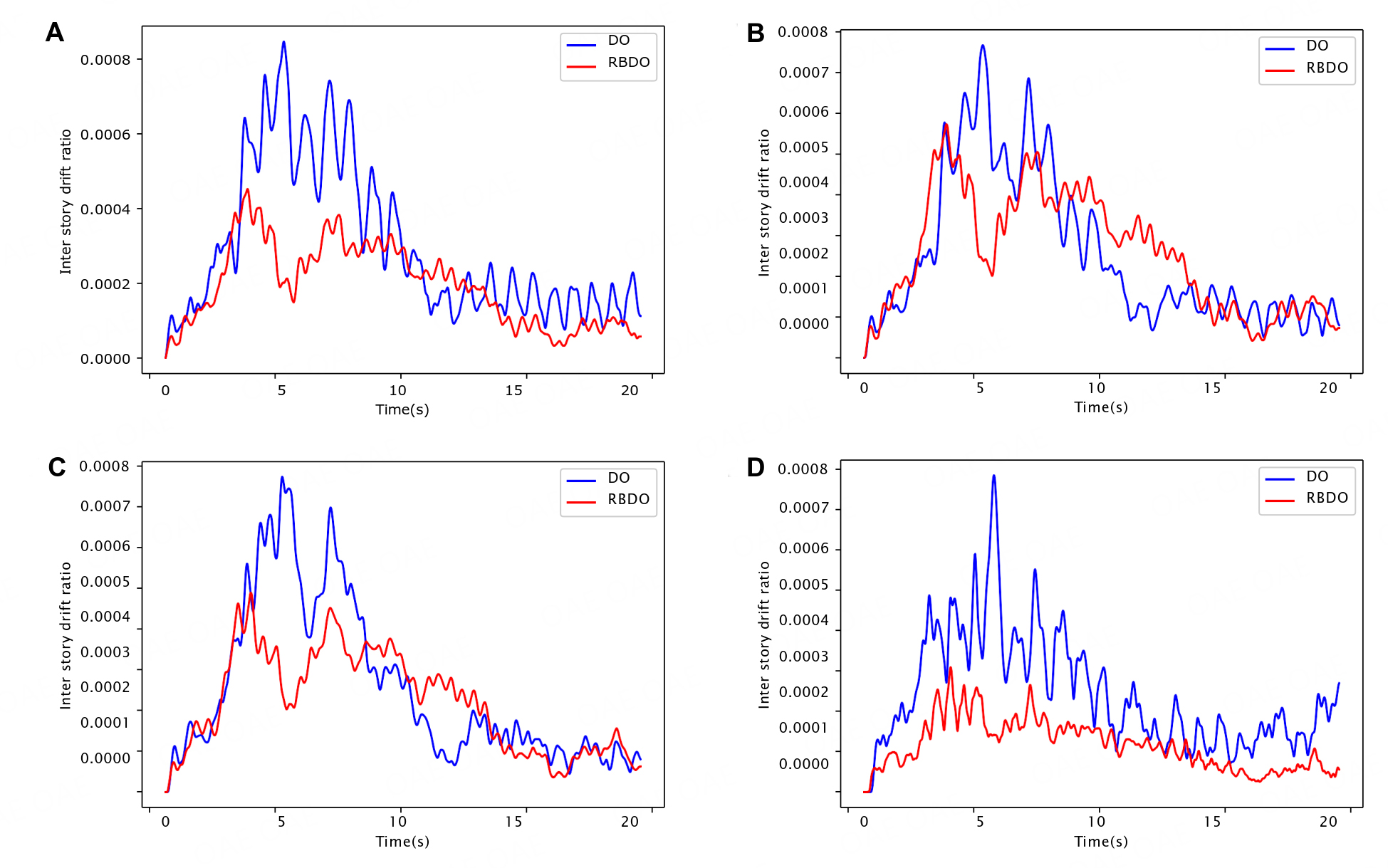
The root-mean-square time histories of the inter-story drift ratios of several floors for the optimal results obtained through deterministic and reliability-based optimization are depicted in Figure 7. Notably, the optimal outcome of RBDO showcases a substantial reduction in drift ratios compared to the deterministic optimization results, all while maintaining superior global reliability for the structure and incurring only a slight increase in cost. It is evident that the drift ratio of the structure comfortably meets the design requirements, as its root-mean-square time history remains well within the limit of
Multi-objective optimization using NSGA-II
In this section, our aim is to introduce greater flexibility in design optimization, offering a spectrum of solutions for achieving a balanced trade-off between cost and reliability without degrading any of them. Utilizing NSGA-II, which stands for non-dominated sorting GA for multi-objective optimization, allows us to expand beyond the single global value generated by GA, introducing multiple solutions that serve as a Pareto set. The concept of Pareto dominance involves an exhaustive comparison of each solution with every other solution in the population. If no other solution dominates, it is considered non-dominated and is selected by NSGA-II to be part of the Pareto front set. While GA focuses on scalar optimization by providing a single outcome, multi-objective optimization provides a vector, enabling a holistic approach to objectives. Here, we emphasize minimizing structural cost while maximizing reliability. Originally, reliability was utilized only as a constraint in single-objective optimization; however, in this section, we have integrated an additional objective for maximizing reliability. The constraint remains unchanged at
The optimization process involved a population of 100 candidates across 100 generations, yielding the results depicted in Figure 8. Adhering to the constraint
The computational times for different optimization methods are tabulated in Table 3. The computational system utilized an Intel(R) Xenon (R) Gold 5218R CPU @2.10 GHz with 30 logical processors and 127 GB RAM. A marginal increase in time occurred due to the utilization of Python to run the MATLAB code using a MATLAB engine API within Python for reliability analysis. For the deterministic analysis, only response spectrum static analysis was employed. However, for RBDO, 221 deterministic time history analyses were conducted for each fitness check, and their outcomes were then processed in MATLAB for reliability analysis, which extended the time. The multi-objective optimization took approximately 119705.03 seconds, around 96% longer than the single-objective optimization, which consumed 60949.07 seconds. The deterministic analysis required only about 156.9 seconds due to a single static analysis per fitness check. However, it is worth noting that the computational time for reliability analysis was significantly reduced through the adoption of PDEM over classical reliability methods, substantially reducing the number of samples needed for each reliability analysis.
Comparison of computational time for different optimization procedures
| Deterministic optimization | Single-objective optimization using GA | Multi-objective optimization using NSGA-II | |
| Computational time (seconds) | 156.9 | 60949.07 | 119705.03 |
CONCLUSION
In this study, a framework for RBDO is outlined, which combines the PDEM and GA to address global reliability concerns in the context of physically motivated ground motions. The global reliability, which takes into account multiple limit states related to the interstory drift ratio of each floor, is streamlined using the EEV event criteria within PDEM. As a result, an optimal design that ensures sufficient reliability under fully non-stationary ground motion conditions is attained, and a Pareto front set is further obtained to provide flexibility in the trade-off between cost and reliability.
The findings reveal a significant advantage of RBDO over deterministic optimization. The optimal results obtained through deterministic optimization account for only half of the desired reliability level when subjected to stochastic ground motions but come at a cost equivalent to 76.16% of the reliability-based optimal design. In contrast, for a relatively modest 31% increase in cost, the RBDO approach delivers the desired level of reliability against the same stochastic ground motions. This highlights the importance of the RBDO procedure, emphasizing its efficiency and accuracy in achieving reliable designs. Moreover, multi-objective optimization broadens the spectrum of available solutions, meeting the established reliability constraint and ultimately amplifying the quest for flexible and optimal designs. Furthermore, the study demonstrates the advantage of utilizing a physically motivated stochastic ground motion model over the power spectral models and spectral representation method coupled with MCS. The physically motivated model allows for the generation of random ground motions with assigned probabilities, achieved by partitioning the probability space. Consequently, the RBDO process benefits from reduced computational burden compared to the alternative method.
While the RBDO procedure results in a reliable and optimal design, the study acknowledges that even more logical designs can be achieved by incorporating control systems to mitigate seismic hazards. Future investigations will focus on these control systems, including the use of viscous dampers and base isolation systems, to further enhance structural resilience against earthquakes.
DECLARATIONS
Acknowledgments
The support of the Committee of Science and Technology of Shanghai, China (Grant No. 21ZR1425500) and the Ministry of Science and Technology, China (Grant No. SLDRCE19-B-26) is highly appreciated.
Authors' contributions
Software, investigation, implementation, numerical analysis, and formal analysis: Shrestha S
Critical input, supervision, visualization, validation, writing - review & editing, and resources: Peng Y
Availability of data and materials
Some or all data and materials that support the findings of this study are available upon reasonable request.
Financial support and sponsorship
Committee of Science and Technology of Shanghai, China (Grant No. 21ZR1425500) and the Ministry of Science and Technology, China (Grant No. SLDRCE19-B-26)
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2023.
REFERENCES
2. Ghobarah A. Performance-based design in earthquake engineering: state of development. Eng Struct 2001;23:878-84.
3. Dawei Z, Jinyu Z, Chunqiu L, Zhiling W. A short review of reliability-based design optimization. In: IOP Conference Series: Materials Science and Engineering. vol. 1043; 2021. p. 032041.
4. Sullivan TJ, Welch DP, Calvi GM. Simplified seismic performance assessment and implications for seismic design. Earthq Eng Eng Vib 2014;13:95-122.
5. Vrouwenvelder ACWM. Developments towards full probabilistic design codes. Struct Safe 2002;24:417-32.
6. Ministry of Housing and Urban-rural Development of the People's Republic of China. GB 50011-2010: Code for seismic design of buildings; 2010. Available from: https://www.chinesestandard.net/PDF.aspx/GB50011-2010.
8. Peng Y, Ma Y, Huang T, De Domenico D. Reliability-based design optimization of adaptive sliding base isolation system for improving seismic performance of structures. Reliab Eng Syst Safe 2021;205:107167.
9. Aloisio A, Contento A, Alaggio R, Briseghella B, Fragiacomo M. Probabilistic assessment of a light-timber frame shear wall with variable pinching under repeated earthquakes. J Struct Eng 2022;148:04022178.
11. Zhao YG, Ono T. A general procedure for first/second-order reliability method (FORM/SORM). Struct Safe 1999;21. Available from: https://www.sciencedirect.com/science/article/abs/pii/S0167473099000089.
12. Hu Z, Du X. Reliability-based design optimization under stationary stochastic process loads. Eng Optimiz 2016;48:1296-312.
13. Hu Z, Mansour R, Olsson M, Du X. Second-order reliability methods: a review and comparative study. Struct Multidiscipl Optimiz 2021;64:3233-63.
14. Youn BD, Choi KK, Park YH. Hybrid analysis method for reliability-based design optimization. J Mech Des 2003;125:221-32.
15. Yang M, Zhang D, Jiang C, Han X, Li Q. A hybrid adaptive Kriging-based single loop approach for complex reliability-based design optimization problems. Reliab Eng Syst Safe 2021;215:107736.
16. Yang M, Zhang D, Han X. New efficient and robust method for structural reliability analysis and its application in reliability-based design optimization. Compu Meth Appl Mech Eng 2020;366:113018.
17. Yang M, Zhang D, Jiang C, Wang F, Han X. A new solution framework for time-dependent reliability-based design optimization. Compu Meth Appl Mech Eng 2024;418:116475.
18. Wang L, Zhao Y, Liu J. A Kriging-based decoupled non-probability reliability-based design optimization scheme for piezoelectric PID control systems. Mech Syst Sig Process 2023;203:110714.
19. Meng Z, Li G, Wang BP, Hao P. A hybrid chaos control approach of the performance measure functions for reliability-based design optimization. Comput Struct 2015;146:32-43.
20. Rubinstein RY, Kroese DP. Simulation and the monte carlo method. 1st ed. Wiley Series in Probability and Statistics. Wiley; 2016.
21. Peng Y, Chen J, Li J. Nonlinear response of structures subjected to stochastic excitations via probability density evolution method. Adv Struct Eng 2014;17:801-16.
22. Wang L, Zhou Z, Liu J. Interval-based optimal trajectory tracking control method for manipulators with clearance considering time-dependent reliability constraints. Aero Sci Techn 2022;128:107745.
23. Li J, Chen J. The principle of preservation of probability and the generalized density evolution equation. Struct Safe 2008;30:65-77.
24. Li J, Chen J, Fan W. The equivalent extreme-value event and evaluation of the structural system reliability. Struct Safe 2007;29:112-31.
25. Chen J, Li J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters. Struct Safe 2007;29:77-93.
26. Wang D, Li J. Physical random function model of ground motions for engineering purposes. Sci Chin TechnScie 2011;54:175-82.
27. Ai XQ, Li J. Random model of earthquake ground motion for engineering site basing on stochastic physical process. In: International Collaboration in Lifeline Earthquake Engineering 2016. Shanghai, China: American Society of Civil Engineers; 2017. pp. 390–95.
28. Zhangjun L, Xinxin R, Zixin L. Performance-based global reliability assessment of a high-rise frame-core tube structure subjected to multi-dimensional stochastic earthquakes. Earthq Eng Eng Vib 2022;21:395-415.
29. Marano GC, Rosso MM, Aloisio A, Cirrincione G. Generative adversarial networks review in earthquake-related engineering fields. Bull Earthquake Eng 2023; doi: 10.1007/s10518-023-01645-7.
30. Safaeian Hamzehkolaei N, Miri M, Rashki M. An enhanced simulation-based design method coupled with meta-heuristic search algorithm for accurate reliability-based design optimization. Eng Comput 2016;32:477-95.
31. Shayanfar M, Abbasnia R, Khodam A. Development of a GA-based method for reliability-based optimization of structures with discrete and continuous design variables using OpenSees and Tcl. Finite Eleme Anal Des 2014;90:61-73.
32. Zou XK, Chan CM. Optimal drift performance design of base isolated buildings subject to earthquake loads. Comput Aid Optim Des Struct 2001:VⅡ.
33. Zou XK. Integrated design optimization of base-isolated concrete buildings under spectrum loading. Struct Multidisc Optim 2008;36:493-507.
34. Zou XK, Wang Q, Li G, Chan CM. Integrated reliability-based seismic drift design optimization of base-isolated concrete buildings. J Struct Eng 2010;136:1282-95.
35. Lu DG, Song PY, Yu XH. Analysis of global reliability of structures: FORM vs. HOMM. In: Safety, Reliability, Risk and Life-Cycle Performance of Structures & Infrastructures. London; 2013.
36. Castaldo P, Miceli E. Optimal single concave sliding device properties for isolated multi-span continuous deck bridges depending on the ground motion characteristics. Soil Dynam Earthq Eng 2023;173:108128.
37. Peng Y, Ding L, Liu J, Chen J. Probabilistic analysis of seismic mitigation of base‐isolated structure with sliding hydromagnetic bearings based on finite element simulations. Earthqu Eng Resili 2023;2:194-210.
38. Sun P, Peng Y. Probabilistic design optimization of TMDI system for seismic mitigation subjected to stochastic ground motions. Dublin, Ireland; 2023. Available from: http://www.tara.tcd.ie/bitstream/handle/2262/103432/submission_355.pdf?sequence=1.
39. Peng Y, Ghanem R, Li J. Generalized optimal control policy for stochastic optimal control of structures: GENERALIZED CONTROL POLICY FOR STOCHASTIC OPTIMAL CONTROL. Struct Control Health Monit 2013;20:187-209.
40. Xian J, Su C, Guo H. Seismic reliability analysis of energy-dissipation structures by combining probability density evolution method and explicit time-domain method. Struct Safe 2021;88:102010.
41. Chen JB, Lin PH, Li J. First-passage reliability evaluation based on the probability density evolution of stochastic processes. In: Vulnerability, Uncertainty, and Risk. Liverpool, UK: American Society of Civil Engineers; 2014. pp. 782–91.
42. Miceli E, Castaldo P. Robustness improvements for 2D reinforced concrete moment resisting frames: Parametric study by means of NLFE analyses. Struct Concr 2023:suco.202300443.
43. Zou X. Optimal seismic performance-based design of reinforced concrete buildings. The Hong Kong University of Science and Technology; 2002. Available from: https://xueshu.baidu.com/usercenter/paper/show?paperid=157f0xs0cj580xd0v2590630hw418322.
45. Mazzoni S, McKenna F, Scott MH, Fenves GL. OpenSees command language manual. Berkley: University of California; 2006. Available from: http://opensees.berkeley.edu/manuals/usermanual.
46. Fragiadakis M. Response spectrum analysis of structures subjected to seismic actions. In: Beer M, Kougioumtzoglou IA, Patelli E, Au ISK, editors. Encyclopedia of Earthquake Engineering. Berlin, Heidelberg: Springer Berlin Heidelberg; 2013. pp. 1–18.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Shrestha S, Peng Y. Reliability-based design optimization for seismic structures considering randomness associated with ground motions. Dis Prev Res 2023;2:23. http://dx.doi.org/10.20517/dpr.2023.35
AMA Style
Shrestha S, Peng Y. Reliability-based design optimization for seismic structures considering randomness associated with ground motions. Disaster Prevention and Resilience. 2023; 2(4): 23. http://dx.doi.org/10.20517/dpr.2023.35
Chicago/Turabian Style
Shrestha, Subik, Yongbo Peng. 2023. "Reliability-based design optimization for seismic structures considering randomness associated with ground motions" Disaster Prevention and Resilience. 2, no.4: 23. http://dx.doi.org/10.20517/dpr.2023.35
ACS Style
Shrestha, S.; Peng Y. Reliability-based design optimization for seismic structures considering randomness associated with ground motions. Dis. Prev. Res. 2023, 2, 23. http://dx.doi.org/10.20517/dpr.2023.35
About This Article
Copyright
Data & Comments
Data

 Cite This Article 9 clicks
Cite This Article 9 clicks
















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.