Unconditional and conditional simulation of nonstationary and non-Gaussian vector and field with prescribed marginal and correlation by using iteratively matched correlation
Abstract
In many probabilistic analysis problems, the homogeneous/nonhomogeneous non-Gaussian field is represented as a mapped Gaussian field based on the Nataf translation system. We propose a new sample-based iterative procedure to estimate the underlying Gaussian correlation for homogeneous/nonhomogeneous non-Gaussian vector or field. The numerical procedure takes advantage that the range of feasible correlation coefficients for non-Gaussian random variables is bounded if the translation system is adopted. The estimated underlying Gaussian correlation is then employed for unconditional as well as conditional simulation of the non-Gaussian vector or field according to the theory of the translation process. We then present the steps for augmenting the simulated non-Gaussian field through the Karhunen-Loeve expansion for a refined discretized grid of the field. In addition, the steps to extend the procedure described in the previous section to the multi-dimensional field are highlighted. The application of the proposed algorithms is presented through numerical examples.
Keywords
1. INTRODUCTION
Probabilistic analysis and reliability estimation often require the unconditional and conditional simulation of the correlated non-Gaussian vector of random variables with the prescribed marginal probability distribution and correlation coefficients. The use of the simulated samples for uncertain propagation or reliability analysis for civil engineering problems is well illustrated in several textbooks[1-3]. The simulation could be carried out by modeling the random variables using the Nataf translation system (or theory of translation process or normal to anything)[3-6], which represents the joint probability distribution of the vector of random variables by the Gaussian copula[7] and probability transformation. The simulation can also be based on normal polynomials[8-11]. A key component of the modeling is to evaluate underlying Gaussian correlation coefficients based on the prescribed correlation coefficients for the non-Gaussian random variables[12-15]. This underlying Gaussian correlation is governed by a double integral equation. Since the analytical solution for the underlying Gaussian correlation is only available under very special circumstances, the underlying characteristics are frequently evaluated using an iterative procedure and numerical integration methods. Moreover, given a correlation coefficient for the non-Gaussian random variables, there is no guarantee that one can find the underlying Gaussian correlation based on the Nataf translation system[12, 13, 16]. An additional problem for the modeling that needs to be dealt with is that the nearest correlation matrix[17, 18] may need to be employed since there is no guarantee that the derived underlying Gaussian correlation matrix from the translation process is positive semi-definite.
Besides simulating the non-Gaussian vector of random variables, the simulation of nonstationary/nonhomogeneous and non-Gaussian random fields is also of importance for structural reliability estimation[19]. Two popular methods to simulate the random field are the spectral representation method (SRM) and the method based on the Karhunen-Loeve (KL) expansion. SRM[20-22] is based on the spectral characteristics of the random field in the time domain, space domain, or both. The spectral characteristics of the field are defined by the power spectral density (PSD) function obtained by using Fourier transform. SRM was extended to simulate nonstationary/nonhomogeneous and non-Gaussian fields[5, 23-26]. These studies use iterative procedures to find the underlying Gaussian PSD function; the PSD and autocorrelation (AC) function forms a Fourier pair (i.e., Wiener - Khintchine theorem). The sampled Gaussian field using the underlying Gaussian PSD function can then be mapped to the non-Gaussian domain based on the theory of the translation process. SRM was extended for conditional simulation in several studies[27-30] for stationary/nonstationary processes and fields based on the conditional joined Gaussian distribution function.
The KL expansion is a special case of the orthogonal series expansion[31]. The orthogonal functions in KL expansion are obtained from the eigenfunctions of a Fredholm integral equation of the second kind with the autocovariance function as the kernel[19]. A random field is represented by the KL expansion with random coefficients. There are many studies focused on simulating the random field based on the KL expansion with engineering applications[19, 32-36]. Since the sum of the KL expansion with random coefficients leads to the Gaussian process, an iterative procedure was proposed[32, 33] to simulate the non-Gaussian process. It includes sampling many sets of random fields, and updating the simulated fields by modifying and shuffling random expansion coefficients based on ranking in each iteration. The adequacy of the sampled field is judged based on the closeness between the marginal distribution of the sampled field and its prescribed distribution. The use of numerical integration to evaluate the underlying Gaussian correlation function for a non-Gaussian field was considered in several studies[6, 35]. They sampled the Gaussian field based on the underlying Gaussian correlation function and mapped the sampled field to the non-Gaussian field. The disadvantages of using different methods, including the numerical integration method, are discussed in the literature[6].
In the present study, we propose a new sample-based iterative procedure to estimate the underlying Gaussian correlation or its nearest correlation matrix for a non-Gaussian vector or process. We use the estimated underlying Gaussian correlation to simulate the non-Gaussian vector or field according to the theory of the translation process. We then proposed the steps for augmenting the simulated non-Gaussian field through the KL expansion for a refined discretized grid of the field. We also outline the necessary steps for the conditional simulation of the non-Gaussian field. In the following, we first describe the steps used to evaluate the underlying Gaussian correlation for a non-Gaussian process and simulate the non-Gaussian process. We then describe the steps to augment the simulated field using the KL expansion and the formulations for the conditional simulation. The proposed simulation-based iterative procedure to evaluate the underlying Gaussian correlation and its use to carry out unconditional and conditional simulation is illustrated through several numerical examples.
2. EVALUATE THE UNDERLYING GAUSSIAN CORRELATION AND SIMULATION
2.1. Estimating the underlying Gaussian correlation and unconditional simulation
Consider a one-dimensional random field
Since, in many practical applications, the data collection and data analysis for a random field is carried out at discrete points with a given sampling interval. Let
If the marginal CDF is Gaussian and
where
However, if the prescribed marginal distribution is not Gaussian,
where
a)
b)
c) The maximum and minimum values of feasible correlation coefficients
Once
For those elements in
We note that
A verification that the underlying Gaussian correlation matrix
Based on the above description, the proposed simulation procedure in the present study for the non-Gaussian vector or field is summarized as follows:
1. Sample the
2. Evaluate
3. Calculate the underlying Gaussian correlation coefficients
4. Form the underlying Gaussian correlation matrix
5. Apply Cholesky decomposition[40] to
A flowchart showing the above steps are presented in Figure 1, where the panel for conditional simulation is to be discussed in the following sections. The procedure can be applied to the homogeneous/nonhomogeneous non-Gaussian process as well as a vector of the non-Gaussian random variables, as mentioned earlier.
2.2. Sampling of the simulated field by using the KL expansion
In the previous section, it is considered that the marginal CDF and the correlation function are prescribed for the nonhomogeneous non-Gaussian field. Moreover,
The use of
For completeness and in order to provide the background for the conditional simulation based on the KL expansion, the use of the KL expansion is summarized below. In general, the random field (Gaussian or non-Gaussian)
where
By considering that the series shown in Equation (7) is truncated to the first few terms, an approximation to
By taking advantage of the availability of
where
By applying
2.3. Conditional simulation
Consider that the field to be simulated
Let
where
This matrix can be constructed by rearranging
By generating
We also note that a method[34] was developed to carry out the conditional simulation of the Gaussian field based on the KL expansion. It can be shown that their method for the underlying Gaussian random field at
where the eigenvalue
and
where
Once
2.4. Discussion on the extension to the multi-dimensional random field
In this section, we highlight steps to extend the procedure described in the previous section to the
Since the extension to the multi-dimensional field is straightforward, no further consideration for the
3. ILLUSTRATIVE EXAMPLES
3.1. Examples of using the proposed procedure to evaluate underlying Gaussian correlation and unconditional simulation
Several numerical examples are presented by considering the homogeneous/nonhomogeneous processes with weakly and strongly non-Gaussian processes to illustrate the applicability of the proposed procedures depicted in Figure 1.
The examples in this subsection were considered in the literature[32, 35]. The assumed marginal distributions and the AC function for the homogeneous non-Gaussian cases (i.e., Cases 1 to 8) are listed in Table 1. The use of the beta distribution described in the table leads to a weakly non-Gaussian field, while the use of the lognormal distribution described in the table results in a strongly non-Gaussian field.
Definition of the cases (see [35])
| Case | Prescribed autocorrelation function for homogeneous and nonhomogeneous cases Cases 1 to 4 are homogeneous Cases 4 to 8 are nonhomogeneous | Distribution type and notes | |
| Beta distribution | Lognormal distribution | ||
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
First, for each of the considered homogeneous cases, the application of the proposed procedure shown in Figure 1 is employed. For the analysis, samples of the independent standard normally distributed random variables are simulated for a sample size
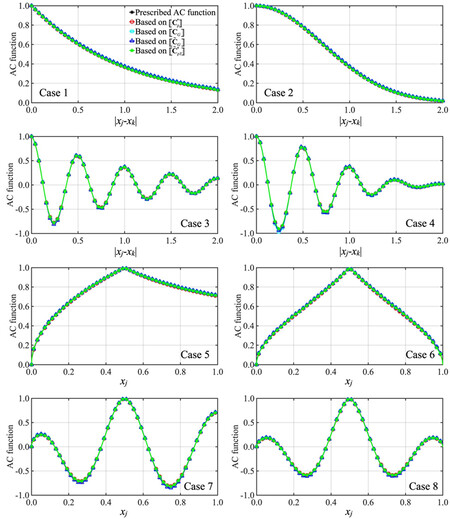
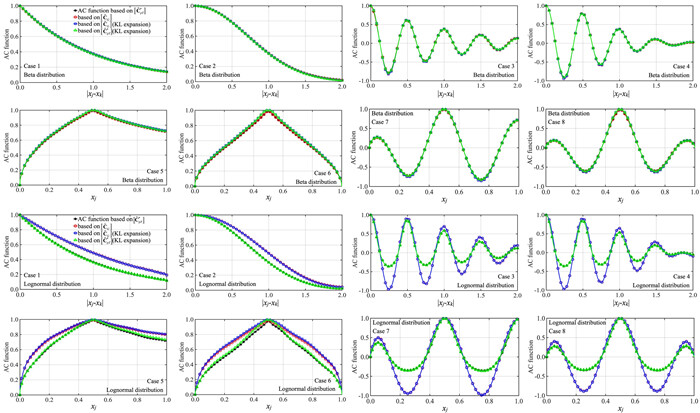
Figure 2. Comparison of the prescribed AC function, estimated AC function based on samples, and underlying Gaussian AC function for Cases 1 to 8 by considering that the marginal distribution is the beta distribution shown in Table 1. The plots for Cases 5 to 8, considered
Figure 3. Comparison of the prescribed AC function, estimated AC function based on samples, and their differences for Cases 5 to 8. The considered marginal distribution is the beta distribution shown in Table 1. AC: Autocorrelation.
The results presented in Figure 2 and Figure 3 indicate that the underlying Gaussian AC functions are close to the target AC functions. The closeness is because the use of the beta distribution presented in Table 1 as the marginal distribution leads to only weakly non-Gaussian fields for the considered cases. The weakly non-Gaussian behavior was noted in the literature[35]. For Cases 2 and 4 (for the considered grid system), it is observed that
The plots for Cases 5 to 8 shown in Figure 2 are those calculated for
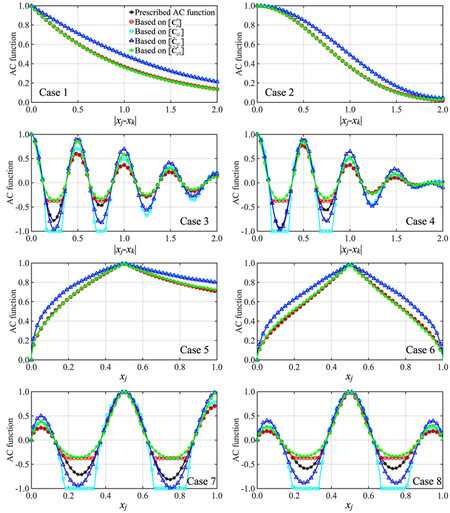
By repeating the analysis that is carried out for the results presented in Figure 2 and Figure 3 but replacing the beta distribution with the lognormal distribution shown in Table 1, the obtained results are shown in Figure 4 and Figure 5. As pointed out in the study[35], the use of this lognormal distribution results strongly non-Gaussian field. This strongly non-Gaussian behavior is reflected in the calculated underlying Gaussian AC functions.
Figure 4. Comparison of the prescribed AC function, estimated AC function based on samples, and underlying Gaussian AC function for Cases 1 to 8 by considering that the marginal distribution is the lognormal distribution shown in Table 1. The plots for Cases 5 to 8, considered
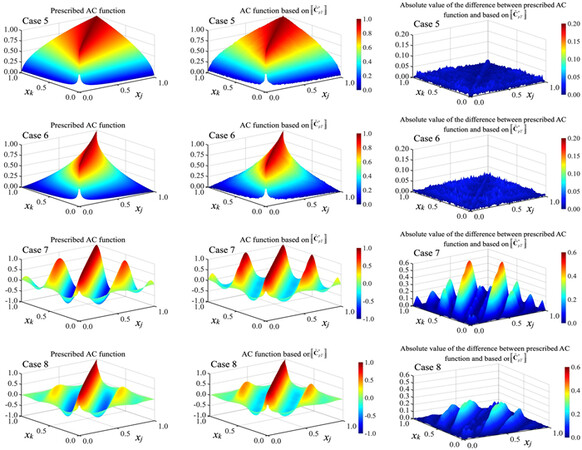
Figure 5. Comparison of the prescribed AC function, estimated AC function based on samples, and their differences for Cases 5 to 8. The considered marginal distribution is the lognormal distribution shown in Table 1. AC: Autocorrelation.
The plots presented in Figure 4 for Cases 3, 4, 7, and 8 indicate that there are segments where
The plots presented in Figure 4 for Cases 3, 4, 7, and 8 show that
Figure 5 shows the surface of the target AC functions and the surface of the underlying Gaussian AC functions. In the same figure, the differences between the surface of the target AC function and the surface of
3.2. Examples using the KL expansion to simulate non-Gaussian field
In this subsection, we consider again all cases shown in Table 1 but use the KL expansion to augment the simulated field. For the analysis, we take advantage of the availability of
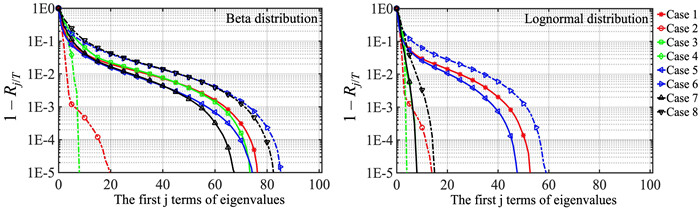
First, the eigendecomposition is applied to
Figure 6. Value of
We use the obtained
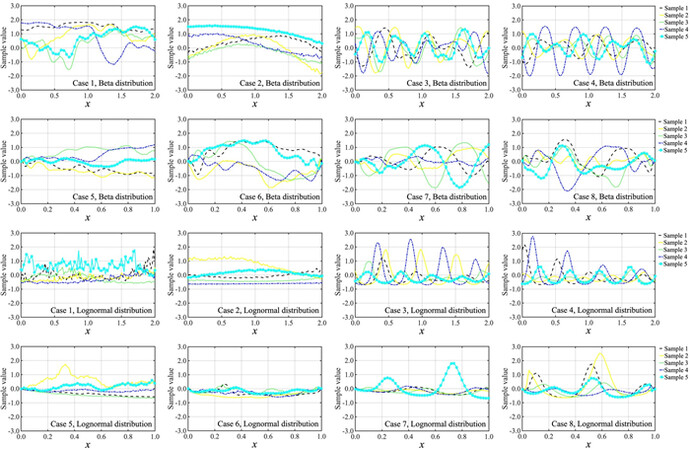
Figure 7. Typical samples obtained by applying the KL expansions and probability transformation mapping for each of the cases listed in Table 1. The first two rows are obtained by considering the beta distribution presented in Table 1 and the last two rows are obtained by considering the lognormal distribution presented in Table 1. KL: Karhunen-Loeve.
Figure 8. Comparison of the calculated correlation coefficient from the sampled random field to
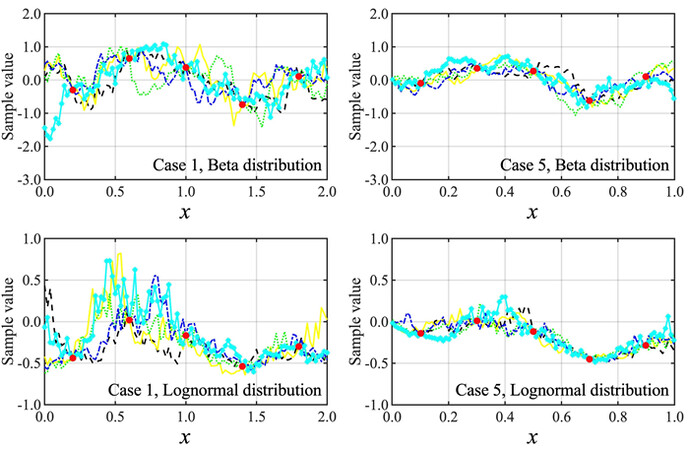
3.3. Examples of conditional simulation
For illustrating the conditional simulation, we consider Cases 1 and 5. By assuming that the marginal distribution is the beta or lognormal distribution shown in Table 1, we sample a field at
4. CONCLUSIONS
A sample-based numerical procedure to estimate the underlying Gaussian correlation for a homogeneous/nonhomogeneous non-Gaussian field is proposed in the present study. The estimation is based on the Nataf translation framework and takes advantage that the range of feasible correlation coefficients for non-Gaussian random variables by using the translation is bounded. Numerical examples show that the proposed estimation procedure is effective and can be used directly to identify whether the underlying Gaussian correlation that leads to exactly matching the prescribed correlation can be found. It is shown that by taking into account the bounds, the underlying Gaussian correlation can be easily found by using the simple bisection method or optimization algorithm. From the numerical example, it was noted that
We also present the steps to augment the simulated non-Gaussian field for a refined discretized grid of the random field by applying the KL expansion and using samples obtained for a much more coarse grid system. The procedure is illustrated through numerical examples.
It was shown that the conditional simulation could easily be carried out within the established simulation framework, and the extension of the procedure to the multi-dimensional random field case is straightforward.
DECLARATIONS
Acknowledgments
We gratefully acknowledge the financial support received from the Natural Sciences and Engineering Research Council of Canada (RGPIN-2016-04814, for HPH), the China Scholarship Council (No. 201807980004 for MYX), and the University of Western Ontario.
Authors' contributions
Investigation, Methodology, Formal analysis, Writing - original draft, Writing - review & editing: Xiao MY
Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Writing - original draft, Writing - review & editing: Hong H
Availability of data and materials
Some or all data, models, or code generated or used during the study are available from the author by request.
Financial support and sponsorship
The authors acknowledge the financial support received from the Natural Sciences and Engineering Research Council of Canada (RGPIN-2016-04814, for HPH) and the China Scholarship Council (No.201807980004, for MYX).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Ang AHS, Tang WH. Probability concepts in engineering planning and design, vol. 2: Decision, risk, and reliability. New York, NY, USA: John Wiley & Sons, Inc.; 1984.
2. Madsen HO, Krenk S, Lind NC. Methods of structural safety Mineola, New York: Dover Publications, Inc.; 2006.
3. Melchers RE, Beck AT. Structural reliability analysis and prediction. New York, NY, USA: John Wiley & Sons, Inc.; 2018. Available from: https://www.wiley.com/en-hk/Structural+Reliability+Analysis+and+Prediction%2C+3rd+Edition-p-9781119265993 [Last accessed on 9 May 2022].
4. Nataf A. Determination des distribution don t les marges sont donnees. Comptes Rendus Acad Sci 1962;225:42-3.
5. Grigoriu M. Simulation of stationary Non-Gaussian translation processes. J Eng Mech 1998;124:121-6.
6. Chen H. Initialization for NORTA: Generation of random vectors with specified marginals and correlations. INFORMS J Comput 2001;13:312-31.
7. Embrechts P, McNeil AJ, Straumann D. Correlation and dependence in risk management: properties and pitfalls. In: Dempster MAH, editor. Risk management: value at risk and beyond. Cambridge: Cambridge University Press; 2002. pp. 176-223.
10. Zhao Y, Zhang X, Lu Z. A flexible distribution and its application in reliability engineering. Reliab Eng Syst Saf 2018;176:1-12.
11. Lu Z, Zhao Z, Zhang X, Li C, Ji X, Zhao Y. Simulating stationary non-gaussian processes based on unified hermite polynomial model. J Eng Mech 2020;146:04020067.
12. Li ST, Hammond JL. Generation of pseudorandom numbers with specified univariate distributions and correlation coefficients. IEEE Trans Syst Man Cybern 1975;SMC-5:557-61.
13. Liu P, Der Kiureghian A. Multivariate distribution models with prescribed marginals and covariances. Probabilist Eng Mech 1986;1:105-12.
14. Lurie PM, Goldberg MS. An approximate method for sampling correlated random variables from partially-specified distributions. Manag Sci 1998;44:203-18.
15. Yang I. Distribution-free Monte Carlo simulation: premise and refinement. J Constr Eng Manag 2008;134:352-60.
16. Cario MC, Nelson BL. Modeling and generating random vectors with arbitrary marginal distributions and correlation matrix, technical report. Evanston, IL: Department of Industrial Engineering and Management Sciences, Northwestern University; 1997. [Last accessed on 9 May 2022].
17. Higham NJ. Computing the nearest correlation matrix - a problem from finance. IMA J Numer Anal 2002;22:329-43.
18. Qi H, Sun D. A quadratically convergent newton method for computing the nearest correlation matrix. SIAM J Matrix Anal Appl 2006;28:360-85.
19. Ghanem RG, Spanos PD. Stochastic finite elements: a spectral approach. Mineola, NY, USA: Courier Corporation; 2003. Available from: https://link.springer.com/book/10.1007/978-1-4612-3094-6 [Last accessed on 9 May 2022].
20. Shinozuka M, Jan C. Digital simulation of random processes and its applications. J Sound Vib 1972;25:111-28.
22. Shinozuka M, Deodatis G. Simulation of multi-dimensional gaussian stochastic fields by spectral representation. Appl Mech Rev 1996;49:29-53.
23. Yamazaki F, Shinozuka M. Digital generation of non-Gaussian stochastic fields. J Eng Mech 1988;114:1183-97.
24. Deodatis G, Micaletti RC. Simulation of highly skewed non-Gaussian stochastic processes. J Eng Mech 2001;127:1284-95.
25. Ferrante F, Arwade S, Graham-brady L. A translation model for non-stationary, non-Gaussian random processes. Probabilist Eng Mech 2005;20:215-28.
26. Shields M, Deodatis G. Estimation of evolutionary spectra for simulation of non-stationary and non-Gaussian stochastic processes. Comput Struct 2013;126:149-63.
27. Vanmarcke EH, Fenton GA. Conditioned simulation of local fields of earthquake ground motion. Struct Saf 1991;10:247-64.
28. Kameda H, Morikawa H. Conditioned Stochastic processes for conditional random fields. J Eng Mech 1994;120:855-75.
29. Hu L, Xu YL, Zheng Y. Conditional simulation of spatially variable seismic ground motions based on evolutionary spectra. Earthq Eng Struct Dyn 2012;41:2125-39.
30. Cui XZ, Hong HP. Conditional simulation of spatially varying multicomponent nonstationary ground motions: bias and Ill condition. J Eng Mech 2020;146:04019129.
31. Zhang J, Ellingwood B. Orthogonal series expansions of random fields in reliability analysis. J Eng Mech 1994;120:2660-77.
32. Phoon K, Huang S, Quek S. Simulation of second-order processes using Karhunen-Loeve expansion. Comput Struct 2002;80:1049-60.
33. Phoon K, Huang H, Quek S. Simulation of strongly non-Gaussian processes using Karhunen-Loeve expansion. Probabilist Eng Mech 2005;20:188-98.
34. Ossiander ME, Peszynska M, Vasylkivska VS. Conditional stochastic simulations of flow and transport with karhunen-loève expansions, stochastic collocation, and sequential gaussian simulation. J Appl Math 2014;2014:1-21.
35. Kim H, Shields MD. Modeling strongly non-Gaussian non-stationary stochastic processes using the iterative translation approximation method and Karhunen-Loève expansion. Comput Struct 2015;161:31-42.
36. Zheng Z, Dai H. Simulation of multi-dimensional random fields by Karhunen-Loève expansion. Comput Methods Appl Mech Eng 2017;324:221-47.
37. Anderson TW. An introduction to multivariate statistical analysis (Vol. 2). New York, NY, USA: Wiley; 2003. pp. 5-13.
38. Stuart A, Arnold S, Ord JK, O'Hagan A, Forster J. Kendall's advanced theory of statistics New York, NY, USA: Wiley. Inc.; 1994.
39. Tong YL. The Multivariate normal distribution. New York, NY, USA: Springer; 1990. pp. 181-201.
40. Higham NJ. Analysis of the cholesky decomposition of a semi-definite matrix. Oxford University Press; 1990. Available from: http://eprints.maths.manchester.ac.uk/1193/1/high90c.pdf [Last accessed on 9 May 2022].
41. Stefanou G. The stochastic finite element method: Past, present and future. Comput Methods Appl Mech Eng 2009;198:1031-51.
42. Xiu D. Numerical methods for stochastic computations: a spectral method approach. Princeton University Press; 2010. Available from: https://dl.acm.org/doi/book/10.5555/1893088 [Last accessed on 9 May 2022].
43. Gerbrands JJ. On the relationships between SVD, KLT and PCA. Pattern Recognition 1981;14:375-81.
44. Baraniuk R. Compressive sensing. IEEE Signal Process Mag 2007;24:118-21.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Xiao MY, Hong HP. Unconditional and conditional simulation of nonstationary and non-Gaussian vector and field with prescribed marginal and correlation by using iteratively matched correlation. Dis Prev Res 2022;1:5. http://dx.doi.org/10.20517/dpr.2022.01
AMA Style
Xiao MY, Hong HP. Unconditional and conditional simulation of nonstationary and non-Gaussian vector and field with prescribed marginal and correlation by using iteratively matched correlation. Disaster Prevention and Resilience. 2022; 1(1): 5. http://dx.doi.org/10.20517/dpr.2022.01
Chicago/Turabian Style
Xiao, M. Y., H. P. Hong. 2022. "Unconditional and conditional simulation of nonstationary and non-Gaussian vector and field with prescribed marginal and correlation by using iteratively matched correlation" Disaster Prevention and Resilience. 1, no.1: 5. http://dx.doi.org/10.20517/dpr.2022.01
ACS Style
Xiao, MY.; Hong HP. Unconditional and conditional simulation of nonstationary and non-Gaussian vector and field with prescribed marginal and correlation by using iteratively matched correlation. Dis. Prev. Res. 2022, 1, 5. http://dx.doi.org/10.20517/dpr.2022.01
About This Article
Copyright
Data & Comments
Data
 Cite This Article 48 clicks
Cite This Article 48 clicks














Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.